线性回归方程相关系数r的计算公式 线性回归方程r的大小

线性回归方程r的大小

样本相关系数的定义公式是：　样本相关系数r有以下特点： 1.r的取值介于－1与1之间。 2.当r＝0时，X与Y的样本观测值之间没有线性关系。　 3.在大多数情况下，0＜｜r｜＜1，即X与Y的样本观测值之间存在着一定的线性关系，当r＞0时，X与Y为正相关，当r＜0时，X与Y为负相关。　 4.如果｜r｜＝1，则表明X与Y完全线性相关，当r＝1时，称为完全正相关，而r＝－1时，称为完全负相关。

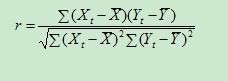
回归分析中r是相关性系数r∈[－1，1]。lrl＝1是确定函数关系，0.75≤丨r丨＜1，相关性较强。0.25≤丨r｜＜0.75相关性一般。丨r丨＜0.25没有相关性

线性回归系数r怎么求

r=∑(Xi-X的平均数)(Yi-Y平均数)/根号下[∑(Xi-X平均数)^2*∑(Yi-Y平均数)^2]

线性回归系数r可以通过计算相关系数得到。相关系数是用来衡量两个变量之间线性关系强弱的统计量，取值范围为-1到1之间。
计算相关系数需要以下步骤：
1. 计算两个变量的协方差，记为cov(X,Y)。
2. 计算两个变量的标准差，记为std(X)和std(Y)。
3. 相关系数r等于协方差cov(X,Y)除以两个变量的标准差的乘积std(X) * std(Y)。
公式为：r = cov(X,Y) / (std(X) * std(Y))
其中，cov(X,Y)代表变量X和变量Y的协方差，std(X)和std(Y)分别代表变量X和变量Y的标准差。
线性回归系数r的取值范围为-1到1，其中，r=1表示两个变量呈完全正相关，r=-1表示两个变量呈完全负相关，r=0表示两个变量之间没有线性关系。

线性回归系数r是通过计算数据的协方差以及各个变量的标准差来求得的。具体步骤如下：
1. 计算每个变量的平均值：找到每个变量的平均值。
2. 计算协方差：计算每个变量之间的协方差。对于变量x和y，协方差可以通过以下公式计算：
cov(x, y) = Σ((x_i - mean(x)) * (y_i - mean(y))) / (n-1)，其中x_i和y_i分别是x和y的第i个观测值，mean(x)和mean(y)是x和y的平均值，n是样本数量。
3. 计算每个变量的标准差：计算每个变量的标准差。标准差是协方差的开方。
4. 计算线性回归系数r：将协方差除以各个变量的标准差的乘积，即可得到线性回归系数r。
r = cov(x, y) / (std(x) * std(y))
线性回归系数r的值介于-1和1之间。如果r为正值，则表示x和y正相关；如果r为负值，则表示x和y负相关；如果r接近于0，则表示x和y之间没有线性关系。

回归系数r计算公式

非标准化的回归系数计算公式为: B1=r×(SDY/SDX) r是皮尔森积差相关系数,是变量Y随着变量X变化的程度,将其乘以Y与X的标准差之比,是考虑到Y与X的不同取值范围。

标准化的回归系数计算公式为:β=r

1. 为：r = cov(x,y) / (std(x) * std(y))2. 这个公式的原理是通过计算自变量x和因变量y的协方差cov(x,y)与它们各自的标准差std(x)和std(y)的乘积之比来得出回归系数r的值。
3. 这个公式是线性回归分析中非常重要的一个计算公式，可以用来评估自变量和因变量之间的相关性，进而进行预测和分析。
在实际应用中，还可以通过调整自变量和因变量的取值范围，来探究它们之间的关系。

首先已知回归系数b1，讲方程逆推，自变量因变量互换，得到回归系数b2，相关系数r=sqr(b1*b2)(sqr是开平方的意思)，如此便可得到相关系数r。

直线回归y=a＋bx跟相关系数r之间没有关系的，回归方程是表述了各点之间自变量与应变量的产业化规律，表达的是一个趋势。相关系数r表态的是这种趋势的相关程度，也就是点的集中程度。如果所有的点距回归方程都很近，说明相关性好。如果点比较分散，|r|的值小，那回归方程的指导意义就不是太大

以上是问答百科为你整理的3条关于线性回归方程相关系数r的问题「线性回归方程r的大小」希望对你有帮助！更多相关线性回归方程相关系数r的计算公式的内容请站内查找。