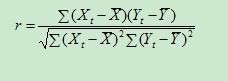相关系数 相关系数r的计算公式

文章目录：

1. 什么是相关系数,相关系数有什么作用?
2. “相关系数”在什么意思?
3. 什么是相关系数

一、什么是相关系数,相关系数有什么作用?

协方差作为描述X和Y相关程度的量，在同一物理量纲之下有一定的作用，但同样的两个量采用不同的量纲使它们的协方差在数值上表现出很大的差异。为此引入如下概念：

定义

 称为随机变量X和Y的相关系数。

定义

若ρXY=0，则称X与Y不相关。

即ρXY=0的充分必要条件是Cov(X，Y)=0，亦即不相关和协方差为零是等价的。

定理

设ρXY是随机变量X和Y的相关系数，则有

（1）∣ρXY∣≤1；

（2）∣ρXY∣=1充分必要条件为P{Y=aX+b}=1，（a，b为常数，a≠0）

二、“相关系数”在什么意思?

相关系数是最早由统计学家卡尔·皮尔逊设计的统计指标，是研究变量之间线性相关程度的量，一般用字母 r 表示。由于研究对象的不同，相关系数有多种定义方式，较为常用的是。

相关系数r的一般在0.8以上，认为A和B有强的。0.3到0.8之间，可以认为有弱的相关性。0.3以下，认为没有相关性。

扩展资料

相关表和相关图可反映两个变量之间的相互关系及其相关方向，但无法确切地表明两个变量之间相关的程度。相关系数是用以反映变量之间相关关系密切程度的统计指标。相关系数是按积差方法计算，同样以两变量与各自的离差为基础，通过两个离差相乘来反映两变量之间相关程度；着重研究线性的单相关系数。

需要说明的是，皮尔逊相关系数并不是唯一的相关系数，但是最常见的相关系数，以下解释都是针对皮尔逊相关系数。

依据相关现象之间的不同特征，其统计指标的名称有所不同。如将反映两变量间线性相关关系的统计指标称为相关系数（相关系数的平方称为）；将反映两变量间曲线相关关系的统计指标称为非线性相关系数、非线性判定系数；将反映多元线性相关关系的统计指标称为复相关系数、复判定系数等。

参考资料：

三、什么是相关系数

相关系数是衡量两个变量之间线性关系强度和方向的统计量。

一、相关系数的定义

相关系数是衡量两个变量之间线性关系强度和方向的统计量。它通过计算两个变量之间的协方差除以它们各自标准差的乘积，得到一个介于-1到1之间的数值。这个数值可以反映两个变量之间的线性关系的紧密程度和方向。

二、相关系数的取值范围

相关系数的取值范围在-1到1之间。当相关系数为-1时，表示两个变量之间存在完全负相关的关系，即一个变量增加，另一个变量减少。当相关系数为0时，表示两个变量之间不存在线性关系，即它们的变化互不影响。

当相关系数为1时，表示两个变量之间存在完全正相关的关系，即一个变量增加，另一个变量也增加。

三、相关系数的意义

相关系数可以帮助我们了解两个变量之间的关系强度和方向。通过计算相关系数，我们可以判断两个变量之间是否存在线性关系，以及这种关系的紧密程度。此外，相关系数还可以帮助我们预测一个变量对另一个变量的影响程度。

在金融市场中，我们可以通过计算不同股票之间的相关系数来构建投资组合，以降低风险并获得更高的回报。

相关系数在各领域的应用

一、相关系数在金融领域的应用

在金融领域，相关系数被广泛应用于风险评估和投资组合管理。通过计算不同资产之间的相关系数，投资者可以了解资产之间的关联程度，从而更好地分散投资风险。股票A和股票B的相关系数较高，说明它们的价格变动趋势较为一致。

那么将它们同时纳入投资组合可能会导致风险无法有效分散。投资者可以通过分析相关系数来调整投资组合，以达到降低风险、提高收益的目的。

二、相关系数在经济学领域的应用

在经济学领域，相关系数被用于衡量两个经济变量之间的关系。例如通货膨胀率和失业率之间可能存在负相关关系，即通货膨胀率上升时，失业率可能下降；反之亦然。通过计算这两个变量之间的相关系数。

经济学家可以更好地理解它们之间的关系，从而为政策制定提供依据。此外，相关系数还可以用于研究其他经济现象，如收入水平与教育程度之间的关系等。

三、相关系数在统计学领域的应用

在统计学领域，相关系数是一种常用的描述变量之间关系的方法。它可以帮助研究者了解变量之间的线性关系强度和方向。相关系数的取值范围为-1到1，其中-1表示完全负相关，1表示完全正相关，0表示无关。

通过计算相关系数，研究者可以判断变量之间是否存在显著关系，以及关系的强度如何。这对于数据挖掘、回归分析等统计任务具有重要意义。

以上是问答百科为你整理的3条关于相关系数的问题，希望对你有帮助！更多相关相关系数的内容请站内查找。